문제 설명
1. 3XN 크기의 벽을 2X1, 1X2 타일로 채우는 경우의 수를 구해보자!
2. 문제 길이가 겁나 짧다... 그냥 이게 다임
풀이 과정
1. DP문제이다. 참 이 문제는...고민할 내용은 정말정말정말정말 많지만 코드로 구현하면 뭐가 이렇게 짧지? 하는 기분을 준다.
2. DP를 푸는 방법은 개인적으로 처음부터 무식하게 들이박는 수밖에 없다고 생각이 든다.
3X1의 타일의 경우는 못구한다.
3X2의 타일의 경우는
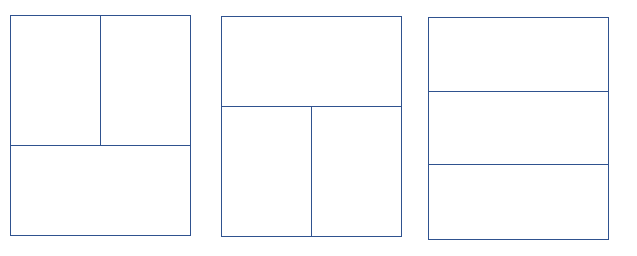
얘네 셋이 나올 것이다.
3X3의 타일의 경우는 못구한다.
3X4의 타일의 경우는 저 위에있는 3X2 타일에다가 추가로 3X2타일을 붙이면 구할 수 있을 것이다.
그런데... 그 방식 말고도 다른 방식으로 타일을 채울 수도 있을 것이다 예를 들어
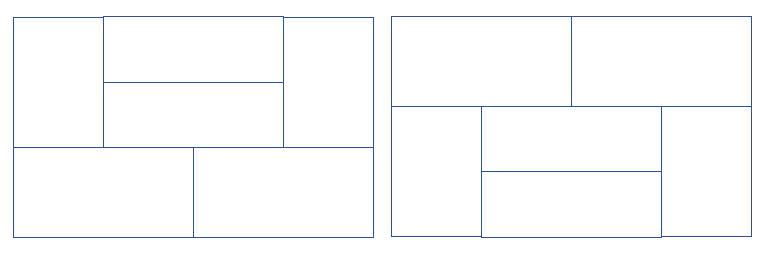
이런 애들이 추가로 나타나게 될 것이다.
더 해보자
3X5의 타일은 못구할 것이다.
DP 좀만 해봤으면 알겠지만, 이쯤 되면 홀수는 걍 못구한다고 생각해주면 될것이다.
3X6의 타일은?
위의 3X4의 타일을 구하는 경우의 뒤에 3X2의 타일을 추가로 붙여 주면 된다고 생각이 들 것이다....
그런데 여기서 주의해야 하는 것이 있다.
3x4의 타일의 뒤에 3x2의 타일을 붙여준다고 생각해 보면, 3x4에서만 만들어지는 특별한 친구들이 3x2타일 뒤에 나타나는 경우가 3x6에 나타날 텐데?? 이거를 놓치지 않을까?? 예를 들자면
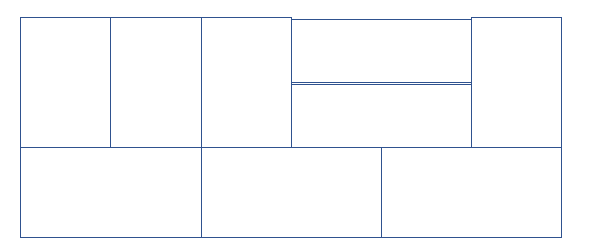
이거.
이거는 3X4의 뒤에 붙여준다고 나오는 친구가 아니다. 그러므로
3X6을 구하려면 3X2에 3X4를 붙여주는 방법도 알아야 할 것이다.
즉, 그 전에 나타난 특별한 타일의 개수 X 그 전전타일 만드는 방법수 를 구해주면 될것이다.
그러면 또 3X6에서만 나타나는 희한한 모양의 친구들이 있지 않을까? 당연히 있다.
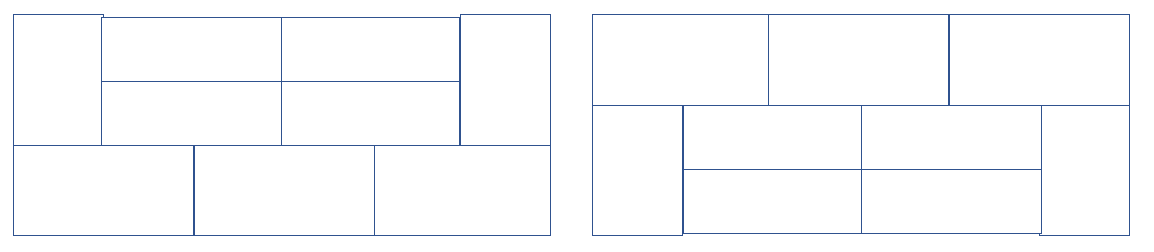
이런 친구들이 있다.
참고로 쟤 모양 확인해 보면 왠지 모르게 데칼코마니 형태이다.
이전에 나타나지 않는 모양인 가운데 타일이 중간의 양옆에 위치하는 모양이다.
아마 나중에 8 10 12 ... 이렇게 가도 저런 친구가 나타나겠지??
여기까지 왔으면 대충 점화실을 세울 수 있을 것이다.
타일은 짝수마다 만들어 낼 수 있으며
1) 이전에 만들어진 짝수번째 타일의 개수 X 3
2) 그 전전의 전체 타일 개수 X 이전타일의 특별한 타일 개수
3) 해당 위치에서 만들어지는 특별한 타일 개수
3. 뭔가 되게 복잡해 보인다....? 근데 이거 사실 별거 없다.
왜냐? 특별한 타일은 매번 2개씩밖에 생기지 않기 때문이다.
4. 자 그럼 구해보면
tile[0] = 1;
for(int i=2; i<=N; i+=2){
tile[i] = tile[i-2]*3;
for(int j=i-4; j>=0; j-=2){
tile[i] += tile[j]*2;
}
}이런 식으로 구하면 될 것이다.
전형적인 식 구하기는 엄청 어려운데 왠지 적으면 쉬워보이는 문제이다....
코드
'알고리즘 공부' 카테고리의 다른 글
| [HackerRank] Jumping on the Clouds java 풀이 (0) | 2024.10.07 |
|---|---|
| [백준 5635번] 생일 - java (0) | 2023.02.03 |
| [백준 14940번] 쉬운 최단거리 - java (0) | 2022.04.19 |
| [백준 12934번] 턴 게임 - java (0) | 2022.04.19 |
| [백준 2258번] 정육점 - java (0) | 2022.04.10 |